ある日、午前中に雪が降り始めた。雪はつねに一定のペースで降る。
除雪車が正午(AM12時)ぴったりに動き出し、1時間で2マイルの除雪を完了し、さらに1時間で1マイルの除雪を完了した。
雪はいつ降り始めた?
※除雪車が雪をかく速さは同じものとする。
ryu.です。
こちらはかなり有名な超ド級に難しい数学クイズの問題として有名であった問題です。Twitterの質問箱の方でフォロワーの方から送っていただきましたし、私自身も聞き覚えはあったもののこうして真剣に取り組むことは初でした。ですのでほぼ初見同然です。
今回の記事ではこの問題について自分の意見を書きつつ、個人的な良問紹介という形で見て行こうかなと思います!季節外れではありますがね(笑)。
解法はぱっと思いつく…?
この問題を解く上での自分の考えを見ていきましょう。
まずは求めたい時刻と雪が単位面積あたりに積もっていく速さをそれぞれ変数にとり、あとは1時間で除雪する雪の量が同じだからそれを見ていこう、と。すると、それぞれ午前\( (12-x)\)時、\(y\)(\(m^3\)/h・mile)でおいたあとに、2回除雪した量を等号で結べば良いものと考えます。すると、除雪する瞬間も雪はどんどんと積もっていくので、それを考慮して題意に沿った式を立てていきます。するとかく雪の量は進むにつれて線形的に大きくなるので、この1時間ずつにそれぞれかく量は\(x,y\)で表すと、
- 最初の1時間:それまでに積もっていた2マイル×\(x\)時間×\(y\)(\(m^3\)/h・mile)=\(2xy\)(\(m^3\))に加え、かいているときに積もる量\(\displaystyle\frac{1}{2}\times 2 \times y=y\)(\(m^3\))が足されて\(2xy+y\)(\(m^3\))
- 次の1時間:それまでに積もっていた1マイル×\( (x+1)\)時間×\(y\)(\(m^3\)/h・mile)=\( (x+1)y\)(\(m^3\))に加え、かいているときに積もる量\(\displaystyle\frac{1}{2}\times 1 \times y=\frac{y}{2}\)(\(m^3\))が足されて\(xy+1.5y\)(\(m^3\))
よってこの二つの量が等しくなるので、二つを等号でつないで整理すると出てくる\(x\)の値は\(y\)に依存することなく\(\displaystyle\frac{1}{2}\)と求められる。したがって、求める答えはAM11:30だ!!!!

実際に解いた時の解答。本当はこれ間違いなんだけどね。
本当にこれで良いのか?
ところが、何かがおかしい。
アレほどややこしそうで難問と噂が立つような問題がここまで簡単に解けるものなのか…?解法としてあまりにシンプルでスッキリした答えになるので少々勘ぐってしまう。そして上の解答を眺めていると、ふと気付くのである。
「除雪車が一定の速さで動くはずがなくないか…?」
そう、一定の時間で除雪車がかく雪の量が一定なら瞬間的に除雪する量も必ず一定である。この図を見れば一目瞭然だが、除雪車自体の速度が一定ならどう考えても後半に行くほど一回で除雪する量が多くなるので問題と矛盾するのである。つまり、何か違うものをパラメータとしてこの問題にアプローチしなければならない。
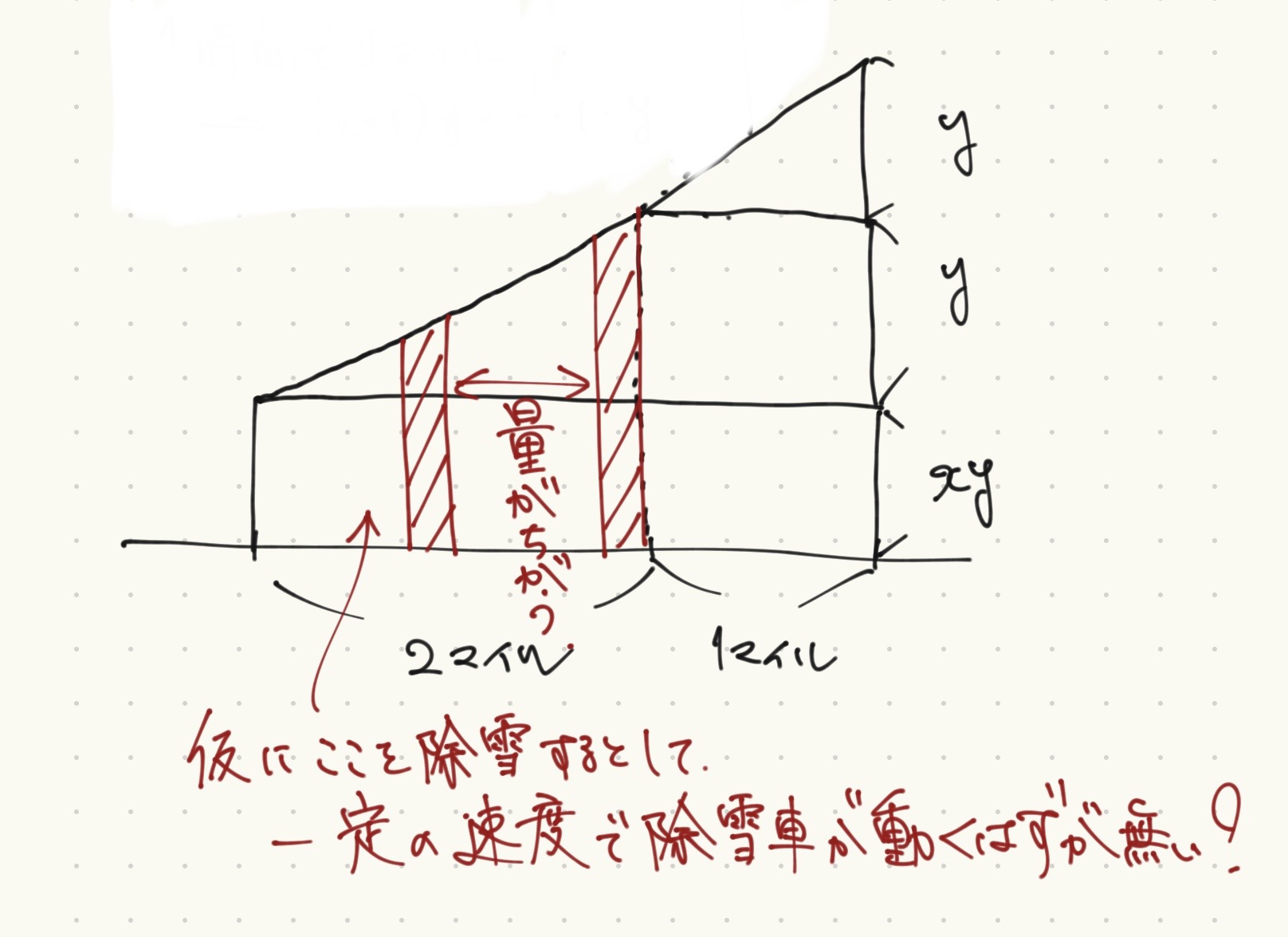
分かりにくい人はこの図(当時のメモ)で考えてみると良い。赤い斜線部を除雪するときに同じ一定の速度と勘違いしていたのが大きなミス。
ここからが多少悩む時間である。さて、どうしたものか…。
結局答えは…
それではきちんとした答えを考えてみよう。先においた二つの変数はそのまま置いておいて、何か違う尺度を使って考えなければならない。
すると、除雪車は毎回新しいところをかくのだから、時間によって瞬間的にかくことのできる量がわかる。午後\(t\)時に除雪車が雪をかくべき量は\( (x+t)y\)である。すると、単位時間あたりにかく量が等しいのならばその時点においての除雪車の速度を考えることができます。したがって瞬間的に\( \displaystyle\frac{1}{(x+t)y}\)マイル進む計算になる。(というか時刻が午後\(t\)時のときの除雪車の速さが\(\displaystyle f(t)=\frac{1}{(x+t)y}\)で表されるということ。)あとはこれを\(t\)について0から1まで、そして1から2まで積分することでそれぞれ2マイルと1マイル進んだことを計算すれば良いことになる。
すると、
$$\frac{1}{2} \int_{0}^{1}\frac{1}{(x+t)y}dt = \int_{1}^{2}\frac{1}{(x+t)y}dt$$
という関係式が立てられ、これを解けば良いことになる。すると、\(y\)に依存することなく\(\displaystyle x=\frac{\sqrt{5}-1}{2}\)と求めることができる。以上より、\(\displaystyle x=\frac{\sqrt{5}-1}{2}\cdot 60 ≒ 37\)分前になることから、答えはAM11:23だ!!!!
まとめ
こういう感じの数学クイズは色々ありますが、ここまで難易度の高い問題は今まで経験したことがありませんでしたし非常に解いていて面白かったです。
コメント