微積物理とは

ryu.です。またもや久しぶりの投稿になってしまい、申し訳ありません。
個人的な話になりますが、MTの免許もしっかりと取って東京の方に戻って参りましたので、ここからは比較的自由にいろんなことを再開できることでしょう。学校もそろそろ始まる関係上、なかなか元の投稿ペースを維持することは難しいとは思いますが、何卒よろしくお願いします。

「微積」を用いた物理

それでは、今回の本題の方に入っていきましょう。
高校で物理を学び、それを受験まで生かしていく人にとっては多少なりとも気になるポイントでしょう。正直にいうと私自身も正確に「微積物理」というものと「定性物理」と勝手に呼んでいるものの区別をできているわけではありませんが、自分なりの考えを書き留めていこうと思います。

そもそも「微積物理」とは？

高校物理を理解する上では定性的に理解して教科書通りに運用していくものと、微分・積分の概念を用いてより詳細に理解していくものとに分かれることでしょう。微分・積分を用いて理解していく方がより正確に定義をしていけるという関係上、難関大を目指す人にとってはある程度避けられないと思いますが、言っても受験に物理を用いる段階を考えるとそこまで難しい概念を用いずとも理解することができるので、これを理解しておく「方がいい」くらいにも言えます。
ものすごく初歩的な一例を紹介しておきましょう。物理を履修した際におそらく最初に扱うであろう公式、等加速度運動についてです。加速度\(a\)、初速度\(v_0\)とした時に時刻\(t\)での速度と変位はそれぞれ
$$v=v_0 + at , x=v_0 t + \frac{1}{2}at^2$$
と表されますが、これはそれぞれ加速度を1回、2回積分して得られたものになります（積分定数は条件付けで一意に決まる）。これは加速度が速度の瞬間の変化率（微分係数）であり、速度が変位の瞬間の変化率（微分係数）であることを考えればわかるでしょう。これを分かっておけば仮に加速度が時間に応じて変化するような場合においても微積分を用いて考えられるようになります。この言い方が正しいのかはわかりませんが、この式を頭に入れておきつつ意味まできっちり理解しておくことがどの分野においても大事だと思います（微積分が必要かどうかは問わない/ドップラー効果などがいい例か）。
実際に問題に使われていたという面で違う例を挙げてみると、今年の東大物理の電磁気の部分がいい例かもしれません。

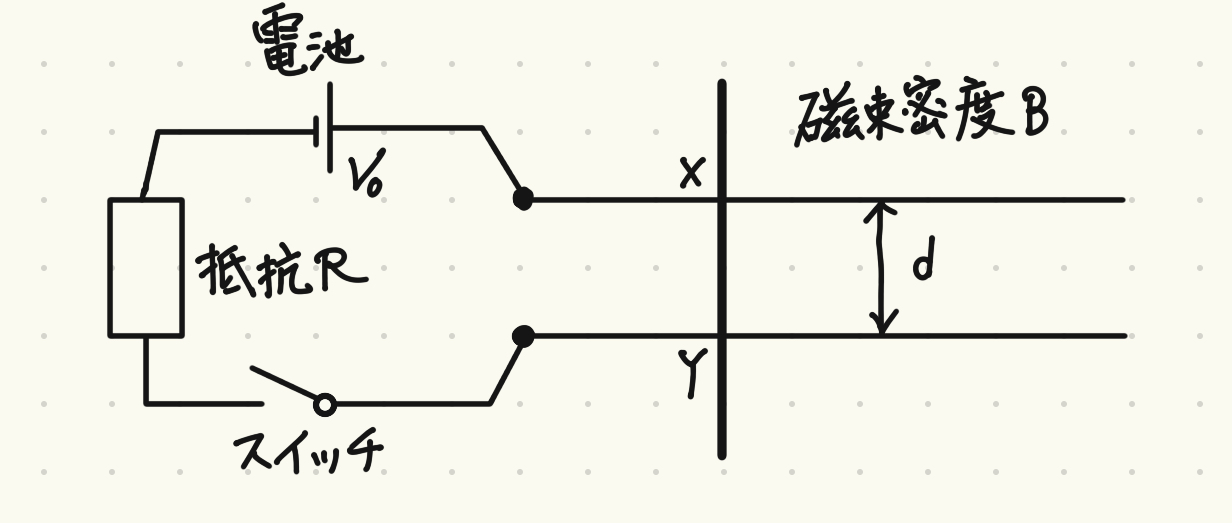
図2-1のように、水平面上に置かれた２本の長い導体のレールの上に、質量\(m\)の導体棒が垂直に渡してある。磁束密度の大きさ\(B\)の一様な磁場が全空間で鉛直方向（紙面に垂直方向）にかけられている。導体棒とレールの接点を\(X,Y\)とし呼ぶ。また、導体棒はレール方向にのみ動けるものとし、摩擦や空気抵抗、導体棒の両端に発生する誘導電荷、および回路を流れる電流が作る磁場の影響は無視できるものとする。
図2-1のように間隔\(d\)の並行なレールの端に電池（起電力\(V_0\)）、抵抗（抵抗値\(R\)）、スイッチを取り付け、導体棒を静止させる。スイッチを閉じた後の様子について以下の設問に答えよ。
※磁束の方向に関しては⑴で問われているが、ここでは本題から逸れるので省略する。なお、導体棒が右に移動することが条件に付加されるのですぐわかるであろう。

図2-1

⑵導体棒に電流\(I\)が流れている時、微小時間\(\Delta t\)の間に、導体棒の速さや接点\(X,Y\)間の起電力はどれほど変化するか。速さの変化量\(\Delta s\)、起電力の変化量\(\Delta V\)を、\(B,d,I,m,R,\Delta t,V_0\)のうち必要なものを使ってそれぞれ求めよ。
⑶スイッチを閉じてから導体棒が到達速さ（注:電流が流れなくなり、導体棒の速さが一定になる時の速さ）に至るまでの間に、導体棒を流れる電気量を、\(B,d,m,R,V_0\)のうち必要なものを使って求めよ。

今回は電磁気的な話についてはほとんど触れないのは先に忠告しておきます。まず⑵に関してですが、こちらは半ば微分を用いた感じになります。もちろん加速度が速度のいわば瞬間の変化量と知っていればいいだけの話なのですが、その知識の根底には微分の概念があると考えて良いでしょう。すなわち、立てる式としては
$$m \cdot \frac{\Delta s}{\Delta t} = IBd$$
となり、ここから求めていくことができます。同じようにして\(\Delta V = \Delta s Bd\)という式を組み立てて求められます。
これに付随して⑶を見ていくと、「瞬間的に流れる電気量が電流の値に一致する、すなわち\(\Delta Q=I\Delta t\)」ということを知っていないと解けません。これに関しては教科書にはっきり載っているわけではない（という記憶ですが間違っていたらごめんなさい！！）ので、電気量を答えないといけないということは積分を利用した考え方をするというのが無難ではないでしょうか。すると、⑵の前半の答えを活かして
$$\Delta Q = \frac{m \Delta s}{Bd}$$
という式になり、これをそのまま積分して、
$$Q = \int_{0}^{s_0}\frac{m}{Bd} ds = \frac{m}{Bd}\cdot\frac{V_0}{Bd}= \frac{mV_0}{(Bd)^2}$$
という答えに辿り着けます。まるっきり微分・積分というわけではありませんが、微積の概念と物理の中への適応のされ方を理解しているだけでかなり解きやすくなる問題と言えるでしょう。
これはほんの初歩とも言える部分になりますが、このようにして微分や積分の概念を中心にして物理現象を説明していこう、というのが「微積物理」と呼ばれるものであり、大学での授業はこれをメインにして物理の講義が進んでいきます。物理現象をより厳密に説明、より精密に理解していくためにはこの微積が必須と言っても過言ではなく、これを理解しておくべきかで受験生が心配をする事態をよく見かけます。しかし、この問題に関しても微積を使った方が劇的に有利というわけではなく、きちんと現象を理解することができれば解くことはできます。もちろん微積を利用した方が理解度が上がりやすい印象ではありますが。

追加：もっとガッツリしたやつ

実際にガッツリとした微積物理について少し余力のある方はここで多少紹介するので、触れてみてください。これを見るとそこまで受験においては高度な微積物理は必要としないことがなんとなくわかると思います…。（鉄緑会の過去問題集ではここまで紹介されていましたが）

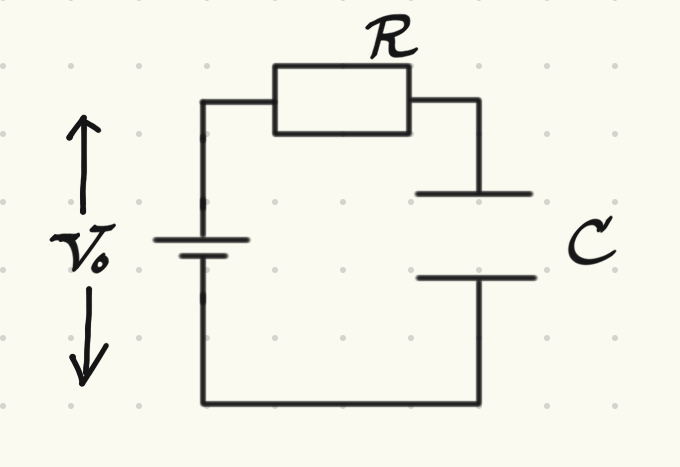ここでは単純な直流電流・抵抗・コンデンサーを直列に繋いだ回路について、そのコンデンサーにたまる電気量を時間経過とともに関数として求めていくという動作を考えます。ちなみに物理を履修している方はもちろんわかると思いますが、\(t=0\)においては\(Q(0)=0\)、\(t \to \infty\)においては\(Q(t) \to CV_0\)となるので、最終的にはこれを用いていきます。
ここで使用するのは一階常微分方程式ですが、これはバリバリ大学数学の内容なので使うタイミングで簡素にわかりやすく説明します。
まずはキルヒホッフの法則に則って回路についての式を立てていきます。すると、時刻\(t\)における電流を\(I(t)\)、電気量を\(Q(t)\)として、
$$V_0-RI(t)-\frac{Q(t)}{C}=0$$
という式になるので、これを\(t\)について1回微分すると、\(\displaystyle\frac{dQ}{dt}=I\)ですから、
$$\frac{dI(t)}{dt}=-\frac{I(t)}{RC}$$
という式が完成します。後はこの関係式を用いて元の\(I(t)\)がどんな式なのか判定していくわけなのですが、そこで用いるのが先に予告しておいた一階常微分方程式です。この式中に出てくる２つの関係を考えると、微分したものと元の関数が同じオーダーになっていることから\(e^x\)を用いて関数が表せるじゃないか！という感じです。すると、これを積分定数\(K\)を用いて解くと、\(\displaystyle I(t)=Ke^{-\frac{t}{RC}}\)という式がうまくこの関係式に合致し（過程は省略）、さらに\(t=0\)における電流の値を使って\(K\)の値を確定させると\(\displaystyle K=\frac{V_0}{R}\)なので、時刻\(t\)における電流\(I(t)\)は\(\displaystyle I(t)=\frac{V_0}{R}e^{-\frac{t}{RC}}\)となることがわかります。これを\(t\)について１度積分したものが蓄積された電気量になるわけですから、特定の時間における値を用いて積分定数を決定しながら求めると、積分定数を\(A\)として、
$$Q(t)=\int\frac{V_0}{R}e^{-\frac{t}{RC}}dt=-CV_0e^{-\frac{t}{RC}}+A$$
となり、\(A=CV_0\)が言えるので、コンデンサーに溜まっていく電気量は\(\displaystyle Q(t)=CV_0 (1-e^{-\frac{t}{RC}})\)となることがわかります。
ただ、この知識を用いたことは受験時全体において1回もありません。つまりこの程度のことすら受験では不必要であり、「微積物理」を完全に必要とするのは少し違うような気がするのです。

実際必要なのかどうなのか…？

さて、内容自体はここまでにしておいて、本題である「微積物理」の是非について考えてみましょう。
正直に言って受験においてはそこまで込み入った微積物理は必要ありません。基本的には演習量をしっかりと確保して、基礎的な公式を理解していればどうにかなるはずです。そもそも物理を学習する上においてわざわざ教科書の範囲を逸脱して微積を用いて勉強していても個人の趣味として学問に打ち込む以外であればまずいりませんし、先の等加速度運動や電気量の変化率が電流に該当する式（\(\Delta Q=I\Delta t\)）やファラデーの電磁誘導の式など、ある程度は教科書を見ても理解が及ぶようにできています。微積で理念を理解することも大事ですが、ひとまずはアウトラインである基礎的な部分をマスターすることが最善手です。その上でこうした理屈をしっかりと理解しようと考えたときにこのように気づいていけば良いでしょう。しかし、難関大生にとっては必要になってくる、というか難関大入試によく対応できるテクニックをしっかりと理解するためには教科書に載っている部分では足りないことも少なくなく、こうした方は場合に応じて理解の補助に活用するという手があります。
角運動量が外力のモーメントに依存するのを外積の微分で求める（\(\displaystyle\frac{dL}{dt}=N\)/本来はベクトル表記）のだとか保存力を周回積分で定義する（\(\displaystyle\oint_C f(r)\cdot dr=0\)）だとか、そこまで進めている方がいるとすれば貴方は素晴らしいと思いますが、それは人に見せびらかそうとしたり周りとの違いに陶酔しようとしたりでやっているのではないでしょう？
俗に言う「微積物理」は受験において必ずしも必要とは言えないでしょう。先に紹介した東大の問題も「ガッツリ微分積分を使わないと解けませーん」という問題ではありませんし、これはどのレベルにとっても同じことだと思います（現に最難関と考えられる『物理　標準問題精講』に関しても微積分を用いた表現はほとんど使用されていません）。しかし、自分で知的探究心や高度な内容の理解を試みようとする場合においては必要に応じて活用を迫られることもあるはずですし、これもどのレベルにも言えると思います。また、実際に入試問題に遭遇した際にも必要な閾値まで実力がついていれば対応可能でしょう。つまり、受験勉強全体で考えたときに物理を学習する際に微積分を強制するべきとは必ずしも言えないのではないでしょうか。ただ、どの道を辿ったとしてもいずれは微積分での物理現象の説明は通過するものでしょうし、そこに関しては肝に銘じておいて欲しいかなとも思います。