ryu.です。
この記事では、以前の図形問題に対する解法の記事にて紹介した問題の答えと、そこまでの思考法について探っていきたいと思います。それでは早速行ってみましょう。
問題１
ある鋭角三角形OABがあり、その外側に\(\angle BOC\)と\(\angle DOA\)が直角になるように直角二等辺三角形△OBC、△ODAを作る。このとき、BDとACは長さが等しく直交することを示せ。
まずはこの問題。教科書にも出てくるレベルである上に、一般的な中学生でも解けるレベルである。一度図に書いて整理してみよう。
すると、線分BCや線分DAを構成している三角形に着目したときに合同関係が使えそうなことがわかるはず。すなわち、合同証明の利用から求めることができる。
\(\triangle AOC\)と\(\triangle DOB\)について考えると、直角二等辺三角形を利用した辺の相等より、\(OA=OD\)と\(OC=OB\)の二つが言える。また、\(\angle AOD\)と\(\angle BOC\)が等しいことから、共通角\(\angle AOB\)を加えて\(\angle AOC=\angle DOB\)が言えるため、以上より二辺夾角相等から\(\triangle AOC\equiv\triangle DOB\)が成り立つことから、対応する辺であることから\(BD=AC\)が成り立つ。さらに直角に交わることを考える段階だが、今見てきた二つの三角形が原点\(O\)を中心に反時計回りに\(90°\)回転させたものであることに気付ければ、そのまま解くことができる。
また、少々高等にはなるが、回転というところを考慮して複素数による利用を用いた解法もある。原点\(O\)を０とし、点AとBにあたる複素数を\(\alpha\)、\(\beta\)と定義する。ここで、点Cは時計回りに点Bを、点Dは反時計回りに点Aをそれぞれ原点周りに\(90°\)だけ回転させた点になる。したがって、それぞれを表す複素数はC(\(-i\beta\))、D(\(i\alpha\))となる。したがって、ベクトルの差と同じ要領でBD、ACを複素数で表すと、BD(\(i\alpha – \beta\))、CA(\(\alpha + i\beta\))となる。ここで、
$$i\alpha – \beta = i ( \alpha + i\beta ) $$
が成り立つことを用いると、BDとACの長さが等しく、BDはACを反時計回りに\(90°\)だけ回転した後に平行移動させた点であることが言える。以上より題意は示された。
この問題については以上である。初等幾何においても複素数においても解くことができ、図形問題の解法が一意に決まるものではないと言うことが実感できてもらえれば良いかなと思う。その中で、図形を整理する段階で適切な解法が見えてくるものだ。
問題２
※著作権の都合により、問題文は省略しています。
この問題は最新の高３駿台模試にて出題された問題だ。図形問題として完成度が良いので採用させてもらった。
今回もまずは図を描いていくことが大切となる。すると、その図を考察していく中で、「線分比を利用して求めていくこと」と「角の二等分線を含む３直線が一点で交わること」の２つに気付ければ、角の二等分線による線分比の一致を利用できることがわかるであろう。これに関しては図を書かないとなかなか気づきことができないため、図の重要性がわかるであろうか。すると、\(\triangle ABC\)と\(\triangle ACD\)を見ると、
$$AB:BC = AE:EC = AD:DC = 1:2$$
となることが容易に言える。ただ、これについては気付くまでが問題なので、これに気付ける目を養っていってほしいと思う。
続いて⑵。これは\(\cos\)、すなわち余弦についての問題なので、予言定理をフル活用していくことには速攻で気付いてほしいところ。逆に⑴を解く段階で余弦定理に目をつけた人もいるであろうが、この問題に目を先に通しておくことで、解法の被り等から使いどきのズレに気づければ良いかと思う。少しそれはどうなのかと思うような視点ではあるものの。
さて、\(AD=x\)ということが分かっているので、\(CD=2x\)である。そこで、\(\triangle ABC\)と\(\triangle ACD\)について余弦定理の式を二回立てると、
$$1^2 + 2^2 – 2\times 1 \times 2\cos\theta = {AC}^2 \\
x^2 + {2x}^2 – 2\times x \times 2x\cos(180°-\theta) = {AC}^2$$
となる。ここで\(\cos (180°-\theta) = \cos \theta\)を利用し、\(AC\)を消去することによって、
$$5-4\cos\theta = 5x^2 + 4x^2\cos\theta$$
となる。これを解いて、
$$\cos\theta = \frac{5(1-x^2)}{4(1+x^2)}$$
と表される。⑴が出来たならこれはたどり着いてほしいところかと思う。
最後に⑶である。四角形\(ABCD\)の面積を求めるので、\(x\)と\(\cos\theta\)の二つの変数を用いて表すのだが、二つは独立ではないので⑵の答えを用いて\(x\)のみの関数として表すことができるので、それをやっていこう。まずは面積だから\(sin\)を求めていくと、四角形\(ABCD\)は円に内接することから正弦の値は必ず正になるので、
$$\sin\theta = \sqrt{1-\cos^2\theta} = \frac{\sqrt{-9x^4+82x^2-9}}{4(1+x^2)}$$
とできるので、これを用いていこう。すると、面積を\(S\)としたときに、
$$S = \frac{1}{2} \cdot 1 \cdot 2 \cdot \sin\theta + \frac{1}{2} \cdot x \cdot 2x \cdot \sin\theta \\
= (1+x^2) \cdot \frac{\sqrt{-9x^4+82x^2-9}}{4(1+x^2)} = \frac{\sqrt{-9x^4+82x^2-9}}{4}$$
となる。そこで、あとは、上の\(x\)の二次関数の最大値を求めに行けば良いので、平方完成により、
$$S = \frac{1}{4}\sqrt{\left(x^2-\frac{41}{9}\right)^2+\frac{1600}{9}}$$
と変形できることから、求める\(x\)の値は\(\displaystyle x^2=\frac{41}{9}\)かつ\(x>0\)なので\(x=\displaystyle\frac{\sqrt{41}}{3}\)であり、面積の最大値は\(\displaystyle \frac{1}{4}\cdot\frac{40}{3}=\frac{10}{3}\)である。これを用いると、\(\displaystyle \cos\theta=-\frac{5 \cdot 32}{4 \cdot 50}=-\frac{4}{5}\)と求められる。最後の方は代数的な処理がメインであったが、最初の着眼点が非常に重要となる問題であるので、こう言った目を養ってほしいというメッセージでもある。
問題３
三角形ABCは半径が\(\displaystyle\frac{1}{2}\)である円に内接しているという条件のもとで、以下の問に答えよ。AB、BC、CAでそれぞれ線分AB、線分BC、線分CAの長さを表す。
(1) \(\angle A=\alpha, \angle B=\beta, \angle C=\gamma\)とおくとき、AB、BC、CAを\(\alpha, \beta, \gamma\)を用いて表せ。
(2) \({AB}^2 + {BC}^2 + {CA}^2\)の最大値を求めよ。
(3) \(AB \times BC \times CA\)の最大値を求めよ。
続いては岐阜大の問題より抜粋。あんまり図形問題っぽくはないのだが…。この問題はまず⑴は解きやすいか。三角形\(ABC\)が円に内接していることと角の大きさを用いて辺の長さを表すことから、正弦定理を用いれば良いことになる。したがって、
$$ 2\cdot\frac{1}{2} = \frac{BC}{\sin\alpha} = \frac{CA}{\sin\beta}= \frac{AB}{\sin\gamma} \\
AB=\sin\gamma, BC=\sin\alpha, CA=\sin\beta $$
と求められる。ここはすんなりきてほしい所。問題はここから。
続いて、⑵を考えていくが、機械的にここまで来れば\({AB}^2 + {BC}^2 + {CA}^2=\sin^2\alpha+\sin^2\beta+\sin^2\gamma\)とそのまま変形できる。後はこれの最大値を求めていけば良いことになるのだが、ここからが難しい所。
まずは三角形の内角の総和が\(180°\)であることを用いれば、\(\gamma\)が容易に消去でき、文字数を２つに減らすことができる。すると、
$${AB}^2 + {BC}^2 + {CA}^2 = \sin^2\alpha+\sin^2\beta+\sin^2(\alpha+\beta)$$
である。ここで少々メタ的な話をすると、対称式の問題は互いの要素が等しくなるように答えが決まりやすい（今回で言えば全部\(60°\)？）上に、この手の問題は角の表記を和や差で表しておくことで求めやすくなる。それを抜きにしても、まずこの状態ではどうしようもないので変形していくことになるが、和積の公式が使いやすい形にしていくことや角の単体の形に分解していくと最大を求められる形からは遠ざかってしまうこと、そして二倍角の公式等により次数を下げていくことなどを思いついて変形していけば良いかと思う。そこで、少し工夫していくことで、
$$\sin^2\alpha+\sin^2\beta+\sin^2(\alpha+\beta) = \frac{1-\cos2\alpha}{2}+\frac{1-\cos2\beta}{2}+1-\cos^2(\alpha+\beta)\\
= 2 – \frac{1}{2} \cdot 2\cos(\alpha+\beta)\cos(\alpha-\beta) – \cos^2(\alpha+\beta) \\
= 2 – \left\{ \cos(\alpha+\beta) + \frac{1}{2}\cos(\alpha-\beta) \right\} ^2 +\frac{1}{4}\cos^2(\alpha-\beta)$$
と、ここまで変形できるだろうか。後は、この式を見るに、\(\displaystyle\left\{ \cos(\alpha+\beta) + \frac{1}{2}\cos(\alpha-\beta) \right\} ^2\)が\(0\)となり、\(\cos^2(\alpha-\beta)\)が最大となる時にこの式全体は最大値を取るということになる。もちろんそれを取りうるような\(\alpha\)、\(\beta\)の値が存在すればの話ではあるが。
すると、内角のとりうる値と\(\cos\)の最大値との関係から、\(\alpha=\beta\)の時に\(\cos^2(\alpha-\beta)\)が最大値\(1\)をとり、これを利用すると、\(\displaystyle\left\{ \cos(\alpha+\beta) + \frac{1}{2}\cos(\alpha-\beta) \right\} ^2\)が\(0\)となるのは\(\displaystyle\cos(\alpha+\beta)=-\frac{1}{2}\)の時である。したがって今までのことより、予想通り\(\displaystyle \alpha=\beta=\gamma=\frac{\pi}{3}\)のときに最大値\(\displaystyle \frac{9}{4}\)を取るという結論が導き出されるということになる。
そして、同じような⑶。今回は積である。つまり、\(AB \times BC \times CA = \sin\alpha\sin\beta\sin\gamma\)となる。今回は⑵と同じようにやっていくとかなり工夫が必要になるが、その解法については後で紹介しよう。ここでは、対称的な式の積の最大値ということから、相加相乗平均の関係式を用いるのが最も早いかと思う。すると、⑵を用いていけば良いことがわかるので、
$$3\sqrt[3]{\sin^2\alpha\sin^2\beta\sin^2\gamma} \le \sin^2\alpha+\sin^2\beta+\sin^2\gamma \le \frac{9}{4}$$
という関係式が得られる。すなわち、
$$\sin\alpha\sin\beta\sin\gamma \le \left(\frac{3}{4}\right)^{\frac{3}{2}} = \frac{3\sqrt{3}}{8}$$
ということが考えられる。後は、実際にこの値を取りうることを確認して（等号成立条件等から）おけばこの答えで良いことは分かるであろう。
また、先に行っていた工夫する解法であるが、⑵と出だしは同じように、
$$\sin\alpha\sin\beta\sin\gamma = \left\{\cos(\alpha-\beta)-\cos(\alpha+\beta)\right\} \cdot \sin(\alpha+\beta)$$
というところまで変形できるとは思うが、ここからが厳しい。ここで\(\alpha+\beta\) による一変数関数に持っていくことを考えると、邪魔となる\(\cos(\alpha-\beta)\)を評価によって消していけば良い。この範囲では\(\sin\)は正に限定されることから、最大値を求めたいので、
$$\left\{\cos(\alpha-\beta)-\cos(\alpha+\beta)\right\} \cdot \sin(\alpha+\beta) \le \left\{ 1 -\cos(\alpha+\beta)\right\} \cdot \sin(\alpha+\beta)$$
というように評価する。すると、\(\cos(\alpha+\beta)=t\)と置き直して右辺（\(\ge 0\)なのでこの操作が容認される）を二乗した式\(f(t)=( 1 -t)^2 (1-t^2)\)が出てくるので、この最大値を微分等によって求めていく。すると、
$$f'(t)= -\frac{1}{2}(t-1)^2(2t+1)$$
ここで定義域を確認すると、\(-1\le t\le 1\)であることより、増減表が右のようになるので、求める最大値は\(\displaystyle\cos(\alpha+\beta)=-\frac{1}{2}\)かつ\(\displaystyle\cos(\alpha-\beta)=1\)のときであり、これは\(\displaystyle \alpha=\beta=\gamma=\frac{\pi}{3}\)のときとして成り立つ。以上より、最大値は\(\displaystyle\frac{3\sqrt{3}}{8}\)となる。
また、この問題については類題が多い上、テクニカルな解法がかなり存在するので、余力のある人はさらに考えてみると良いだろう。
問題４
正三角形ABCの辺AB上に点\(P_1,P_2\)が、辺BC上に\(Q_1,Q_2\)が、辺CA上に\(R_1,R_2\)があり、どの点も頂点に一致していないとする。このとき三角形\(P_1 Q_1 R_1\)と三角形\(P_2 Q_2 R_2\)の重心が一致すれば、<\(P_1 P_2 = Q_1 Q_2 = R_1 R_2\)が成立することを示せ。
ここからはさらに難化していく。この問題は京都大学にて出題されたことのある問題である。
重心の一致を扱っているので、ベクトルか座標平面上だ考えるのが無難だが、ここは簡単に考察できるようにベクトルを採用して解いていこう。座標を用いた解き方だと計算処理がとんでもないことになりかねないためなのだが…。
そして平面上のベクトルなので、一次独立である（線形結合が一意に定められる）ようなベクトルの数は２個であることに注意。３個のベクトル、例えば\(\overrightarrow{OA}\)、\(\overrightarrow{OB}\)、\(\overrightarrow{OC}\)とおいてはいけない。基本的なことだが、ここを疎かにするとかなり減点されることは火を見るより明らかである。そこで、\(\overrightarrow{AB}=\overrightarrow{a}\)と\(\overrightarrow{AC}=\overrightarrow{b}\)の二つのベクトルを設定しておく。すると、ここで互いに異なるパラメータを用いて\(A\)を始点とする各ベクトルを
$$\overrightarrow{AP_1}=p_1\overrightarrow{a}, \overrightarrow{AP_2}=p_2\overrightarrow{a}, \overrightarrow{AR_1}=r_1\overrightarrow{b}, \overrightarrow{AR_2}=r_2\overrightarrow{b} \\
\overrightarrow{AQ_1}=\overrightarrow{a}+q_1\overrightarrow{BC}=\overrightarrow{AQ_1}=(1-q_1)\overrightarrow{a}+q_1\overrightarrow{b}, \overrightarrow{AQ_2}=\overrightarrow{a}+q_2\overrightarrow{BC}=(1-q_2)\overrightarrow{a}+q_2\overrightarrow{b}$$
と定めたときに、重心の座標（ベクトル）が一致するので、
$$\overrightarrow{AG_1}=\frac{1}{3}(\overrightarrow{AP_1}+\overrightarrow{AQ_1}+\overrightarrow{AR_1})=\frac{1}{3}(p_1-q_1+1)\overrightarrow{a}+(q_1+r_1)\overrightarrow{b} \\
\overrightarrow{AG_2}=\frac{1}{3}(\overrightarrow{AP_2}+\overrightarrow{AQ_2}+\overrightarrow{AR_2})=\frac{1}{3}(p_2-q_2+1)\overrightarrow{a}+\frac{1}{3}(q_2+r_2)\overrightarrow{b}$$
とできるので、二つのベクトル\(\overrightarrow{a}, \overrightarrow{b}\)が一次独立であることから、
$$p_1-q_1+1=p_2-q_2+1, q_1+r_1=q_2+r_2$$
であることから、
$$p_2-p_1=q_2-q_1=r_2-r_1$$
が成り立つことにより、この三角形が正三角形であることと、この式から\(P_1 P_2 = Q_1 Q_2 = R_1 R_2\)が成立することが言える。
以上、京大にしては平易な問題ではあったが、ベクトルの基礎を確認する上で非常に有用な問題であろう。
問題５
一辺の長さ４の正方形の中に半径１の円が２つ含まれている。この二つの円が互いに重ならず（接しても良い）正方形の内部を自由に動くとき、それら２円の中心の存在範囲を図示し、その面積を求めよ。
最後に医科歯科大の問題を一つおいていこう。この問題は文中に式関連のものがほとんど存在しないため、設定を自分なりに解釈しておいていく必要がある問題だ。座標を使うのも良いかもしれないが、今回はそれを用いずにやってみる。また、数学の研鑽を積んでいる人ならばこの問題の答え自体は容易にたどり着くことができるかもしれないが、途中の議論を確りとできるかどうかが勝負でもあるので気をつけて。それではまずひとつずつ見ていくようにしよう。
まずは、円の重なりを無視したとしても円の中心が配置できない箇所が存在する。それは正方形の幅\(1\)cmの外縁の部分である。これは説明するまでもないであろう。
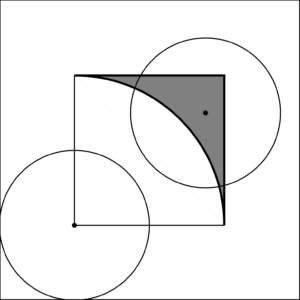そして、次に一方の円をある箇所に固定してもう一つの円が動きうる中心の箇所について考えていく。特例として、まずは正方形の左と下の辺に縁が接している場合から考えていこう。（右図）すると、もう一つの円は、中心同士が２以上離れていることが必要になってくるため、一方の円を中心とする半径\(２\)の円の周上及びその外側というように考えることができる。（右の図の灰色部分）これと同じようにして、元の円を移動させていくことで、これが４つの角にできた配置となる。したがって、その下のような図になるのだが、後はこの面積を求めていくだけである。
そうすると、中学入試レベルの問題に落ち着いていくわけだが、後の計算過程については残念ながら端折らせてもらう。面積を\(S\)とおくと、
$$S= 4\times \left\{ \frac{2^2\cdot\pi}{12}-\left(\frac{2^2\cdot\pi}{6}-\frac{1}{2}\cdot 2^2\cdot \frac{\sqrt{3}}{2}\right) \right\}=4\left(\sqrt{3}-\frac{\pi}{3}\right)$$
と求めることができるというわけである。
まとめ
以上、五問程度図形関連の問題を紹介していったが、いかがだったであろうか。問題の公開から遅れてはしまった上に図形問題？というような問題こそあったとは思うが、図形問題に取り組む良い機会になれば良いと思う。図形問題についてはかなり幅広い視野や経験を必要とするものが多いので、実際に問題として遭遇したときには要注意である。
コメント