物理　応用 pt.1　二体問題と重心系を利用した解き方

ryu.です。
今回は物理の二体問題に関連した内容をまとめていこうかなと思います。二体問題自体を入試問題で問われることはあまりありませんが、これに使われる考え方は難関大において重要になることも多いです。そう言ったものもまとめていきながら紹介していきたいと思います。

二体問題の一般的状況

　それでは本題に入っていこう。今回は二つの質点A、B（質量それぞれ\(m_A, m_B\) ）が存在しており、その位置ベクトル\(\boldsymbol{r_A}, \boldsymbol{r_B}\)を求めていくことを考えていく。なおその二つには相互に引き合う力\(\displaystyle \boldsymbol{F} \)と場による一定の力（重力など）が働いており、それぞれ力の大きさを\(\displaystyle \boldsymbol{f_A}=m_A \boldsymbol{g}, \boldsymbol{f_B}=m_B \boldsymbol{g} \)とおく。もちろん今回はわかりやすいようにこう置いたが、場の力が働かないことも多い。すなわち状況を図で表すとこんな感じだ。（図１）
なお、ボールド体で表されているものは全てベクトルである。一応注意。

まずは重心の概念から考えておこう。二つの質点を一つとして考えたときに、代表させることのできる一点が重心のイメージである。重心を考えたときに、\(m_A + m_B\)がその質量となり、その位置ベクトルを\( \boldsymbol{r_G}\)とおいておく。そうすると運動方程式から、
$$m_A \frac{d ^ 2 \boldsymbol{r_A}}{dt ^2} = \boldsymbol{F}+ m_A \boldsymbol{g} , m_B \frac{d ^ 2 \boldsymbol{r_B}}{dt ^2} = – \boldsymbol{F}+ m_B \boldsymbol{g}$$
が立てられ、同じようにして
$$( m_A + m_B ) \frac{d ^ 2 \boldsymbol{r_G}}{dt ^2} = (m_A + m_B ) \boldsymbol{g}$$
という式も置くことができる。以上三式を総合して（上二式の和と下の式と比較して）考えると、
$$\frac{d ^ 2 \boldsymbol{r_G}}{dt ^2} = \boldsymbol{g}, \boldsymbol{r_G}=\frac{m_A \boldsymbol{r_A}+m_B \boldsymbol{r_B}}{m_A + m_B}$$
と考えられる。すなわち、重心の位置ベクトルは相互に働く力とは関係のない運動で表すことができ、各々の位置ベクトルを用いて表すことができると言うことだ。特に場の力が働いていない時には二質点の重心が静止を含む等速直線運動をするということが言える。

逆に今度は質点Bに対する質点Aの相対的な運動について考察してみよう。二つの加速度の差を取ってみることで、以下のようになる。
$$\frac{d ^ 2 \boldsymbol{r_A}}{dt ^2}-\frac{d ^ 2 \boldsymbol{r_B}}{dt ^2}=\frac{\boldsymbol{F}+ m_A \boldsymbol{g}}{m_A}-\frac{- \boldsymbol{F}+ m_B \boldsymbol{g}}{m_B} = \biggl( \frac{1}{m_A}+ \frac{1}{m_B} \biggr) \boldsymbol{F}$$

ここで、相対位置ベクトルを\(\boldsymbol{r_R}=\boldsymbol{r_A}-\boldsymbol{r_B}\)とおき、さらに換算質量として\(\mu = \displaystyle\frac{m_A m_B}{m_A+m_B}\)と置くことで、上の式を
$$ \mu \frac{d ^ 2 \boldsymbol{r_R}}{dt ^2} = \boldsymbol{F} $$

という形の運動方程式としてみることができる。すなわち相対位置ベクトルの変化を、換算質量と相互に働く力によって（外力となる場の影響を考えずに）この運動方程式を解くことで表せるということになる。後はこの二つを用いてそれぞれの位置ベクトルを以下のようにして表すことができるというわけだ。
$$ \boldsymbol{r_A} = \boldsymbol{r_G} + \frac{m_B}{m_A + m_B}\boldsymbol{r_R} \\
\boldsymbol{r_B} = \boldsymbol{r_G} – \frac{m_A}{m_A + m_B}\boldsymbol{r_R}$$
以上が二体問題のあらかたの解説となる。このように重心とそこからの相対的な運動とに分けて考えることでより運動をわかりやすく捉えることができるというのが二体問題なのである。

例題

ここで一度具体的な題材に触れてみよう。二体問題について若干雰囲気を掴みながらその他の事項についても確認して行って欲しい。

右の図２のように、質点１と質点２がばね定数\(k\)、自然長\(l\)のバネで繋がっている。質点の質量はいずれも\(m\)であるものとする。このうち、高さ\(z=h\)の点に質点１を固定しておき、その真下に質点２を、バネを\(\displaystyle\frac{l}{2}\)だけ縮めた状態で支えておく。なお、鉛直下向き（z軸方向の負の向き）に重力加速度\(g\)が働いており、空気抵抗などは無視できるものとする。
ここから瞬時に質点２の支えを解く。そして、初めて質点２が速度０となったときに質点１の固定を解く。この瞬間を\(t=0\)とする。この後、それぞれの質点の運動について考える。
(1) \(t=0\)のとき、質点２の\(z\)座標を求めよ。
(2) \(t\ge 0\)において、二つの質点の重心の\(z\)座標を\(z_G\)とおく。重心についての運動方程式を立てることで\(z_G\)を\(t\)を用いて表せ。
(3) \(t\ge 0\)において、質点２から見た質点１の相対運動を考える。換算質量を用いて相対運動方程式を立てることで、質点１の相対的な位置ベクトル\(z_R\)を\(t\)を用いて表せ。
(4) 以上の(2)(3)を利用して、質点１の\(z\)座標\(z_1\)と質点２の\(z\)座標\(z_2\)を\(t\)を用いて表せ。
(5) 以上の考察は上のような相対運動の代わりに重心から見た２質点の相対運動を考えることでも求められる。今度はこれを用いて質点１の\(z\)座標\(z_1\)と質点２の\(z\)座標\(z_2\)を\(t\)を用いて表すことをやってみよ。

オリジナル問題なので出来が悪くて申し訳ない。以下、解答をまとめておく。
［解法・解答］
(1) 初期状況でのバネの縮みが\( \displaystyle \frac{l}{2} \)であることから、初めに速度が０となる時は半周期経ってバネの伸びが\(\displaystyle\frac{l}{2}\)となったときである。すなわち、\(t=0\)における質点２の\(z\)座標は\(\displaystyle h-\frac{3}{2}l\)となる。
(2) まず\(t=0\)における重心の\(z\)座標は、
$$\displaystyle z_G = \frac{m \times h + m \times \biggl( h-\frac{3}{2}l \biggr) }{m + m}=h-\frac{3}{4}l $$
と表せる。さらに重心に対しての運動方程式を立てると
$$ (m + m) \frac{d ^ 2 z_G}{dt ^ 2} = -(m + m)g $$
だから、重心は重力加速度\(-g\)で自由落下する。以上から、重心の初速度０も合わせると*1、
$$ z_G = h-\frac{3}{4}l – \frac{1}{2}gt ^ 2 $$
と表せる。
(3) バネの伸びを\(x\)として二質点に対して運動方程式を立てると、
$$ m \frac{d ^ 2 z_1}{dt ^ 2}= -kx-mg \\
m \frac{d ^ 2 z_2}{dt ^ 2}= kx-mg $$
となるので、換算質量\(\displaystyle\frac{1}{2}m\)、相対位置\(z_1 – z_2\)についての運動方程式は
$$ \frac{1}{2}m \times \frac{d ^ 2 (z_1 – z_2)}{dt ^ 2}= -kx$$
となる。すなわち、質点１は質点２に対して単振動をすることがわかる。すると、初速度０、cos型であることを利用して、
$$z_R = l \biggl(1+\frac{1}{2} \cos\biggl( \sqrt{ \frac{2k}{m}}t\biggr)\biggr) $$
と表せる。
(4) 以上のことから、上で述べたこの二式を用いることで最終的に二つの質点の\(z\)座標を求める。
$$ \boldsymbol{r_A} = \boldsymbol{r_G} + \frac{m_B}{m_A + m_B}\boldsymbol{r_R}\\
\boldsymbol{r_B} = \boldsymbol{r_G} – \frac{m_A}{m_A + m_B}\boldsymbol{r_R}$$
これに各々代入することで、
$$ z_1 = h-\frac{1}{4}l – \frac{1}{2}gt ^ 2 + \frac{1}{4} l \cos\biggl( \sqrt{ \frac{2k}{m}}t\biggr) \\
z_2 = h-\frac{5}{4}l – \frac{1}{2}gt ^ 2 – \frac{1}{4} l \cos\biggl( \sqrt{ \frac{2k}{m}}t\biggr)$$
という二式になる。計算は端折ってしまったが。
(5) 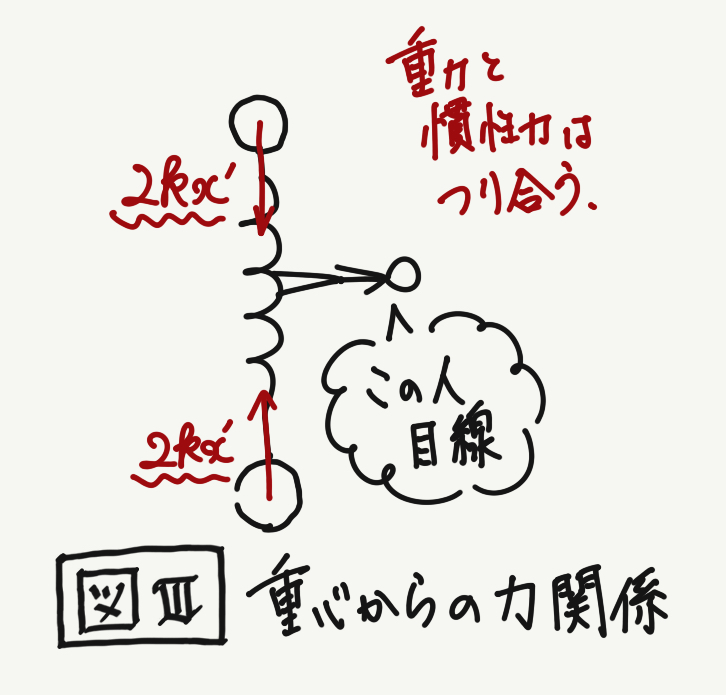今度は重心、すなわちバネの中心を視点としてそこからの慣性系として二質点の運動を考える。つまり右の図３のようになる。このとき、重心に働く重力加速度は各々に働くそれと同じく\(-g\)であるからそれぞれに働く慣性力と重力が釣り合う。そしてバネの伸びを\(x\)とおくと、それぞれの方向に向けての伸びはいずれも\(\displaystyle x’=\frac{1}{2}x\)と考えられるのでばね係数はその辻褄をとって２倍とできる。*2すなわち、それぞれ振幅\(\displaystyle\frac{1}{4}l\)、角振動数\(\displaystyle \sqrt{\frac{2k}{m}}\)の単振動と考えられるから（単振動であることの証明は割愛）、重心からの相対変位はそれぞれ
$$ Z_1 = \frac{1}{2}l + \frac{1}{4}l \cos\biggl(\sqrt{\frac{2k}{m}}t\biggr) \\
Z_2 = -\frac{1}{2}l – \frac{1}{4}l \cos\biggl(\sqrt{\frac{2k}{m}}t\biggr) $$

となる。後はこれを(2)で求めた\(z_G\)に加えることで求める変位が出てくる。

二体問題　補足説明２つ

二体問題に関連して、後二つ紹介しておきたいものがある。
まず、二質点の質量が極端に違う場合には換算質量を求める際に、\(m+M≒M\)が適用できるので、換算質量の式から\(\displaystyle\mu = \frac{mM}{m+M}≒m\)とみなして計算することが可能になる。さらにこの場合は重心の位置が極端に質量が大きい方へよっているため、それに応じた運動の簡略化を考えることも可能になる。詳しい場合はここでは紹介しないが。
そしてもう一つ、運動エネルギーについてだが、以下の式が成り立つ。（重心・相対運動エネルギー保存則と呼んでいるが実際なんと言うかは知らん）
$$ \frac{1}{2}m_A {v_A}^2 + \frac{1}{2}m_B {v_B}^2 = \frac{1}{2}(m_A + m_B) {v_G}^2 + \frac{1}{2} \mu {v_R}^2$$
この証明については実際に各々計算して貰えばわかると思う。これについては大学入試の段階で使用機会があるのかは謎だが。