ryu.です。
今回は初心に立ち返ろう、ということで「基礎の重要性」について書いていこうと思います。勉強に限った話ではないものの、「基礎」がしっかりと定着しているということは非常に重要です。最近Twitterでは非常に基礎的な問題をアンケート機能を通じて確認し合うというのが何故か流行っていますが、正直もう少し正答率が高くてもいいのかなという気はしますね…。まあ投票をしている母集団の差がありますので、なんとも言えませんが。ここで間違えてしまっても、それは「一時の恥」として自分の知識を改めていくという高尚な考えが出来るかどうかが重要だと自分は思います。
そもそも基礎とは
まずはここについて考えていきましょう。勘違いしている人が多いと思いますが、あくまで「基礎」とは簡単な事項のことを単に指しているのでは到底ありません。それを言えば自分が普段から言っているFocus Goldや理科の重要問題集にだって当然難しい問題は入っていますし。そうではなくて、自分としては「基礎」とは難問に出会した際に思考するための「ベース」のようなものと考えています。つまり、何か大きな（サイズ的な意味ではなく）ものを作るために器具の使い方を知るようなもの、と言えば良いですかね。
その中には当然パターン暗記などと言ったものも存在しますが、それ以前の初歩的な部分をきちんと理解しているかは案外基礎固めの段階では軽視されているように思います。もちろんその事実自体は否定するつもりはありませんが、いずれ難問に取り組んでいくとなった時までにはそうした初歩の刷新が必要になってくるものだと自分は実感しています。
難問というのは、高度なテクニックもそうですが、むしろ根本となる「初歩的な基礎」が分かっていないと解けないものなのです。
実際に例を見つつ確認していこう
そこで、実際に自分がTwitter上で問題として出題した三問について少し見ていきましょう。
次のうち、一般的に値が大きいのは
１、静止摩擦力 ２、動摩擦力 ３、これだけでは断定できない
開幕からいきなり物理選択者向けの問題になってしまうのですが、摩擦力についての基本的な理解を問うている問題です。これを間違えている人は普通に出題される力学の問題においても間違う可能性がありますので注意！！
答えは「３、これだけでは断定できない」です。正答率はギリギリ50％に届くかどうかと言ったところでした。おそらく間違えてしまった人は最大静止摩擦力と補完してしまったことによるミスでしょう。もちろん、最大静止摩擦力と動摩擦力で言えば最大静止摩擦力の方が大きいですよ。ただ、静止摩擦力自体は静止する物体に働く外力の合力の大きさに依存するので一般的には動摩擦力との大小は一意に決まらないので注意しましょう。
これについては実際の力学の問題において図の中に摩擦力（静止摩擦力）を「μN」と書いている人は要注意です。あくまでそれは最大の話であり、問題によっては異なってくるので普通に「f」とだけ書いておくことを推奨します。これが摩擦力における基礎的な事実ですし、実際にここまで物理の勉強をしてきた人もこれで問題なかったが故の誤答なのだと思います。ただ、ここから先の問題においてはそれでは通用しない問題もあるかもしれないので、きちんと訂正しておきましょう。
続いてはこちらの特別な四角形と論理説明についての問題です。
四角形ABCDは平行四辺形であるとして、成り立たないのは下のうちどれか。
１、一つの頂点が直角である任意の平行四辺形ABCDは長方形である
２、隣り合う２辺が等しいある平行四辺形ABCDは正方形である
３、同じ長さの対角線が直交するならば平行四辺形ABCDは菱形である
４、上の３つに間違いがある
今回の問題は個人的に想定していた正答率の半分（30％弱）しかなかったのでかなりびっくりしたのですが（というより自分が間違えてる/何か不都合があるのでは？とすら思ってる）、こちらの正解は「４、上の３つに間違いがある」です。つまり、平行四辺形について説明している上の３つは全て合っているということです。こうした問題は去年のセンター試験の「データと分析」の分野でも出ましたし、もしかしたら共通テストにも出る可能性があります。そのため、それぞれの言葉の定義や一度自明に思えるものでも懐疑的に見てみる精神、そしてきちんと論理がわかっているかどうかを今一度確認してみましょう。
では選択肢について一つずつ吟味していきましょう。
まず１つ目。これに入れている人は少なかったです。平行四辺形は対角（向かい側の角）が等しいので、どれか一つの頂点が90°である時点で、辺の長さをどう取ったとしても全ての頂点が直角であることが容易に言えます。これは成立します。
続いて二番。これが一番入れている人が多かったです。ひとまず見てみると、隣り合う２辺が等しい平行四辺形ですから、単純に考えればこの四角形が菱形となり反例があることからこれが誤りだ、と考えがちです。ただ、これについては論理の展開が大事です。今回は「ある」平行四辺形について成り立てば良いので、菱形の範疇に正方形が含まれている以上はこの選択肢も成立するということになります。言い方が悪いのかとも思いましたが、あえて１個目で「任意の」と入れることで差別化をしていますし問題ないと自分は判断しています。これを選んでしまった人は数学においての論理記述「任意の〜・ある〜」や「必要条件・十分条件」などについて一度確認してみましょう。記述式の問題でここの書き間違いをすると大幅減点でしょうし、問題文中に含まれていた場合には０点を喰らうことを想定してもいいような致命的な間違え方です。
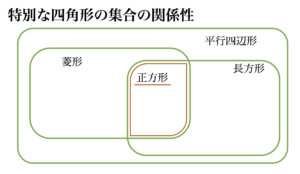そして三番。これに関しては自分はあまり想定していなかったのですが、予想外に回答率が高かった選択肢です。菱形は一般的に同じ長さの対角線にならないのですが、今回は前提条件として同じ長さの対角線を持つものを考えているので、それを判断材料にしている時点でお門違いです。そしてもう一つ間違いを起こしたと考えられるポイントとして、正方形はあくまで菱形の部分集合であるというのがあります。ですので、この定義からいくと「菱形じゃなくて正方形」と考えた方がいるかもしれませんが、「正方形も菱形」なのです。図で表すとこんな感じになります。ちなみに、これは複素数や実数などの集合を考えてみても言えると思います。虚数単位のiがついていれば複素数と考えている人は要注意ですよ？
以上、３つが全て成り立っていることから４が成り立たないということになるわけです。きちんと論理を追っていくことが大切です。
そして最後、これは知らないとかなり誤答してしまいやすい問題でしょう。自分も最初にこの問題が出されたときには間違えましたし。
右のような街路をPからQへ最短距離で移動する。各分岐点で進む方向を等確率に選ぶとして、道中でAを通る確率は下のどれか。ただし、各短辺の長さはいずれも等しいものとする（図を作る技術力のための記述）。
１、2/7 ２、3/8 ３、5/12 ４、18/35
この問題についてですが、まず正解から言いましょう。正解は２番です。ちなみに正答率は３割、そして誘導した４番に６割近くの人が入れていましたね。
この問題をまず考える上で、確率の超基本原理である「確率が同様に確からしいか」がとても大事です。確かに、進み方は全部で35通りで、そのうちAを通過するのが18通りなので一見４番が正しい様に思えます。ただ実はその35通りの起こる確率が全て同様に確からしい、つまり等しいとは言えません。試しに左上の角を通る行き方と右下を通る行き方を考えてみれば選択の余地がある角に到達する回数がそれぞれ3回、4回と異なってくる上に、その確率も1/2がそれぞれにかけられるのでそれぞれ1/8と1/16となります。
ではどう考えれば良いのでしょうか？まず、考え方としてAを通って仕舞えば必ずQには辿り着けますので、PからAに行く確率を考えれば良いことになるのです。そうすると、Aを通過するまでに通るいずれの角においても選択肢は二つ用意されているので、選択の確率はそれぞれ1/2です。したがって選択は4回、行き方は6通りで同様に確からしいので、求める確率は6/16で3/8となるのです。
一見難しい様ですが、確率以外でもこうした根本的に気をつけるor頭に入れておくべき初歩的な原理が存在するのです。その辺りについて、今一度確認してみてはどうでしょう。
まとめ
どうでしょうか。今回出てきた科目に限らず基礎と考えられている部分がいかに重要かということを少しでも分かっていただけたら嬉しいです。もちろん最初にも言いましたが、初学の時点からそうしたことを意識する必要は自分はないと思っています。しかしこうした勉強を進めていく中でいつか刷新していくことも必要でしょうし、そうした機会を見出すのも自分自身の知的好奇心やより多くの題材に触れていくことではないでしょうか。また、どこまでを基礎とするかに絶対的な定義はありませんし、それを議論しては野暮というものです。大事なのは根本から高度な知識までどれだけしっかりと、そして抜けなく頭に入っているかでしょう。これがしっかりしていてこそ後々の思考力が生きてくるのです。
わかり切ったような言い方にはなってしまいましたが、自分は未熟ながらそう考えていましたし今もそうした気持ちで大学の勉強に臨んでいるつもりです。
コメント