ryu.です。
今回は印象深い問題編ということで第二回です。処理力と言えばパッと出てくるのは計算力、ということで東大の過去問から計算処理が死ぬほどキッツい問題を用意しました。正直、相当の処理力がなければ当時この問題を捌き切るのは難しかったのではないでしょうか。
問題：東京大学 2013年 理系数学 第３問（文理一部共通）
A,Bの二人がいる。投げたとき表裏が出る確率がそれぞれ\(\displaystyle\frac{1}{2}\)のコインが一枚あり、最初はAがそのコインを持っている。次の操作を繰り返す。
(ⅰ) Aがコインを持っているときは、コインを投げ、表が出ればAに1点を与え、コインはAがそのまま持つ。裏が出れば、両者に点を与えず、AはコインをBに渡す。
(ⅱ) Bがコインを持っているときは、コインを投げ、表が出ればBに一点を与え、コインはBがそのままもつ。裏が出れば、両者に点を与えず、BはコインをAに渡す。
そしてA,Bのいずれかが2点を獲得した時点で、2点を獲得した方の勝利とする。
例えば、コインが表、裏、表、表と出た場合、この時点でAは1点、Bは2点を獲得しているのでBの勝利となる。
⑴ A,Bあわせてちょうど\(n\)回コインを投げ終えたときにAの勝利となる確率\(p(n)\)を求めよ。
⑵ \(\displaystyle \sum^{\infty}_{n=1} p(n)\)を求めよ。
問題自体は確率が題材なのでその定石に従って数えていくだけなのですが、如何せん計算もそれ以外も処理量が多いです。落ち着いて順番通りに見ていきましょう。
まず、点数が増えるパターンはいずれも表が出るときであり、これを考えると出てくるパターンはここまでに表が計2回出ているパターンか3回出ているパターンのいずれかしか考えられません。したがって、\(n\)を固定していると、2回か3回のいずれかで最終的に勝っているのがどちらかなのかがそもそも変わってきます。したがってAが勝つのは、\(n\)が偶数である時に表が2回出るとき、そして\(n\)が奇数である時に表が3回出るパターンのどちらかになります。これは最終的にAの番で\(n\)回目に表を出すことを考えると、裏が出る回数は総計で偶数にならないといけないからです。
そうすると、それぞれ\(n\)が偶数か奇数かによってそれぞれ考えていきましょう。
まず\(n\)が偶数のとき、\(n=2m\)（\(m\)は自然数）とおいてわかりやすくしてから考えると、\(n\)回目にAが表を出す他にもう一回だけ\(m\)回のAの番で表を出すことを考える必要があります（最後に表を出すときにも二連続でAを出すことを考えて良いのでこれで良い）。そのため、その\(m\)回から1回を選ぶ必要があり、これらを総計して反復試行の確率を求める際の応用によって確率を算出していきましょう。すると、
$$p(n) = m \cdot \frac{1}{2^{2m}} = \frac{n}{2^{n+1}}$$
と確率が求められます。まだこちらは簡単なのですよね…。
続いて\(n\)が奇数のときですが、同じように\(n=2m+1\)（\(m\)は０以上の整数）とおいて考えましょう。今回はAの手番のときにもう1回表を出すのに加えてBの手番のときに1回表が出ている必要があります。すると、どのタイミングでAが表を出すかで\(m\)通り、Bが表を出すタイミングで同じように\(m-1\)通りとなるので、求める確率は
$$p(n) = m(m-1) \cdot \frac{1}{2^{2m+1}} = \frac{n-3}{2} \cdot \frac{n-1}{2} \cdot \frac{1}{2^{n}} = \frac{(n-1)(n-3)}{2^{n+2}}$$
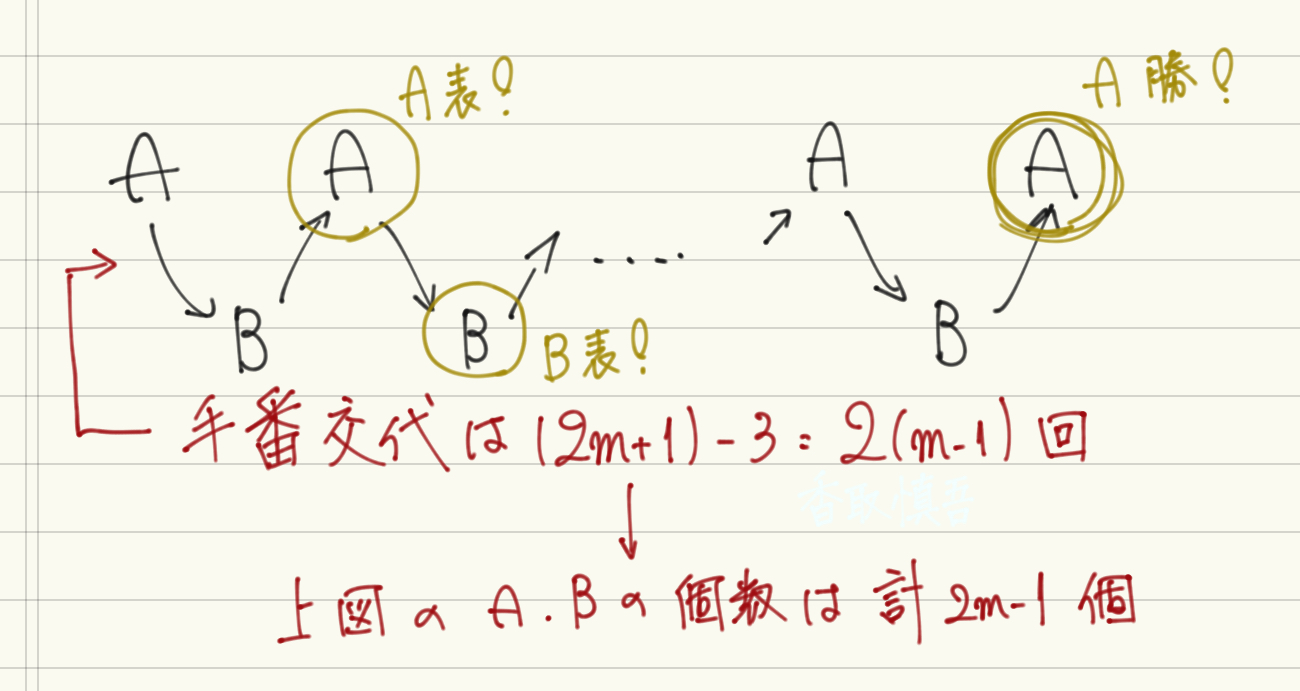となります。ここでAが表を出す〜云々の辺りで困惑する人がいるかもしれませんが、右の図を一例として考えてみてください。交代回数が\(2(m-1)\)回なので、AとBが表を出すチャンスは合計で\(2m-1\)回存在しなくてはなりません。上の思考を考えてみても、合計して同じ数になっていますよね。この考え方でいくと、AとBのどちらが先に表を出すか考えなくて良くなります。以上より、求める確率は
$$p(n) = \frac{n}{2^{n+1}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (n \equiv 0) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ p(n) = \frac{(n-1)(n-3)}{2^{n+2}} \ \ \ \ \ \ \ \ (n \equiv 1) \ \ \ \ \ (\mathrm{mod}\ 2) $$
と求められます。正直ここまで前座なのがまた心を折りますよね…。戦略としてはここまでを着実に解いておいて、後の部分はまた戻ってきてからやるという風にできると良いと思います。
そして理系はここからがこの問題の本番。ただ単に和の極限を計算するだけなので脳死の計算で意外にすぐいけるのでは？と思った受験生を途方もない計算処理の渦に引き込んでは焦りと時間搾取に数学全体の結果ごと沈めてしまいかねない、という悪魔のような問題です。
まず計算ばかりに夢中になっていて論理性でつまずかないようにしましょう。奇数までの和と偶数までの和が極限を取ったときに一致するかどうかを確かめる操作がなければその時点でアウトになることでしょう。今回は先に偶数までの和を求めてから、それに最終奇数項を足すことによって求めていくことにしましょう。偶数までの和についてですが、これは偶奇セットにしてから足し合わせる、すなわち1回目と2回目をセットにという感じで\(2m-1\)回目と\(2m\)回目をセットにして足していくことを考えます。すると⑴で\(m\)をおいて考えていたのが効いてきます。もちろん、奇数の方に関しては\(2m+1\)で考えましたので、こちらのために調整していくことは必要ですが（最初から\(2m-1\)とおいて考えれば良い話ですが、そこまで先読みできるかと言われると怪しいのであえてこちらで書いております）。そうすると、\(\displaystyle S_n = \sum^{n}_{k=1} p(n)\)とおくと、偶数までの和なので\(n=2m\)として
$$\begin{eqnarray} S_{2m} &=& \sum^{2m}_{k=1} p(n) \\
&=& \sum^{m}_{l=1} p(2l) + \sum^{m}_{l=1} p(2l-1) \\
&=& \sum^{m}_{l=1} \biggl\{ \frac{l}{2^{2l}} + \frac{(l-1)(l-2)}{2^{2l-1}} \biggr\} \\
&=& \sum^{m}_{l=1} \frac{2l^2-5l+4}{4^l}\end{eqnarray}$$
と、ここまで計算が進みます。あとはこれを計算するのですが、ここからがまあクソ大変。等比数列の和は問題ないと思いますが、\(\displaystyle \sum^{m}_{l=1} \frac{l^2}{4^l}\)、\(\displaystyle \sum^{m}_{l=1} \frac{l}{4^l}\)の二つが難しいです。
最初に\(\displaystyle \sum^{m}_{l=1} \frac{l}{4^l}\)の方から。これについては典型的なやり方があるので機械的にそれを用いるのでも構いません。実際にここに必要な\(m\)個の項を書き出してみて、もう一つ\(\displaystyle\frac{1}{4}\)をかけたものをそれから引いてみることで計算式がより簡略化します。数式としてプログラムに書き起こすのが非常に面倒だったので手書きになってしまいますが、下の図を参照してみてください。
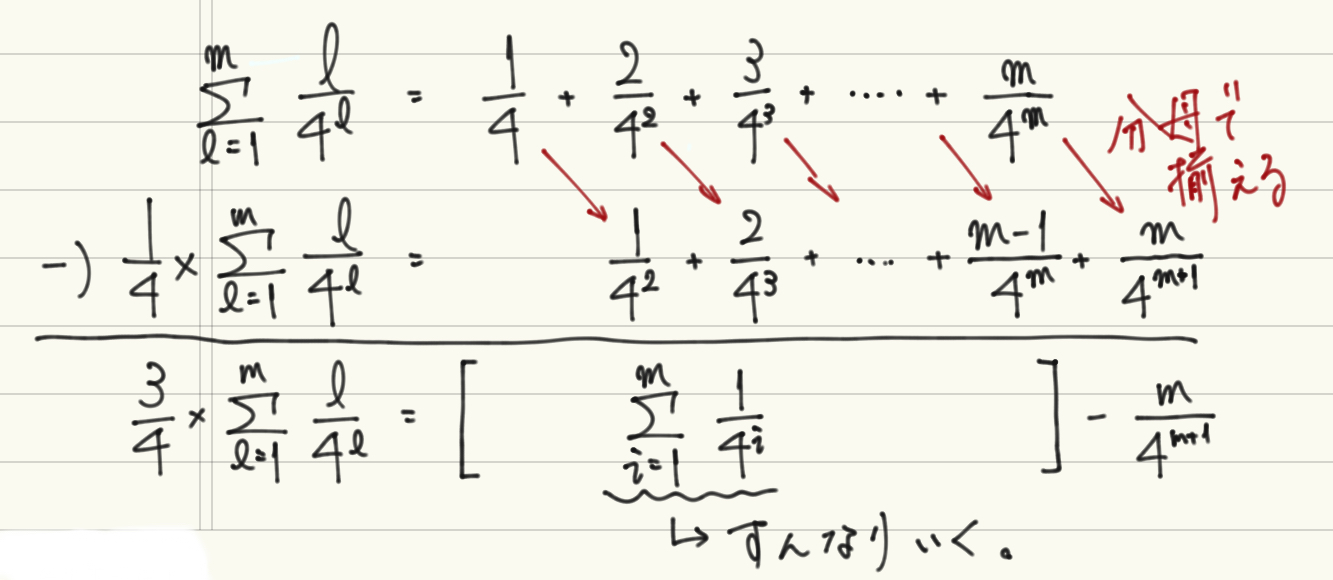
あとはこの図の筆算結果にあるものを利用して、
$$\begin{eqnarray}\sum^{m}_{l=1} \frac{l}{4^l} &=& \frac{4}{3} \biggl\{ \sum^{m}_{i=1} \frac{1}{4^i} – \frac{m}{4^{m+1}} \biggr\} \\
&=& \frac{4}{3} \cdot \frac{1}{3} (1-\frac{1}{4^m}) – \frac{4}{3} \cdot \frac{m}{4^{m+1}} \\
&=& \frac{4}{9} – \biggl(\frac{1}{3} m + \frac{4}{9} \biggr) \frac{1}{4^m} \rightarrow \frac{4}{9}\ \ \ (m \rightarrow \infty ) \end{eqnarray}$$
となります。これを同じような要領で\(\displaystyle \sum^{m}_{l=1} \frac{l^2}{4^l}\)でも行いましょう。すると今度は下の図のようになるので、先の結果と合わせることで求めることができます。
すると、
$$\begin{eqnarray} \sum^{m}_{l=1} \frac{l^2}{4^l} &=& \frac{4}{3} \cdot \biggl\{ 2 \sum^{m}_{i=1} \frac{i}{4^i} – \sum^{m}_{i=1} \frac{1}{4^i} \frac{m}{4^{m+1}} \biggr\} \\
&=& \frac{8}{3} \cdot \sum^{m}_{i=1} \frac{i}{4^i} – \frac{4}{9} + \frac{4}{9 \cdot 4^m} -\frac{m^2}{3 \cdot 4^m} \\
&\rightarrow & \frac{32}{27} – \frac{4}{9} = \frac{20}{27} \ \ \ (n \rightarrow \infty) \end{eqnarray}$$
と求められるんですよね。ここまでが「正しく」求められていれば問題なく解くことができるでしょう。もちろん答えは
$$S_{2m} \rightarrow 2 \times \frac{20}{27} – 5 \times \frac{4}{9} + 4 \times \frac{1}{3} = \frac{16}{27}\ \ \ (m \rightarrow \infty)$$
となります。あとはこれに対して\(S_{2m+1}\)も同じ値へ収束することが求められるので、これで晴れて答えは\(\displaystyle\frac{16}{27}\)となるわけですね。
ちなみに、ここでは\(\displaystyle\lim_{m\to\infty}nr^n=0\)（ただし、\(|r| < 1\)）をしれっと用いていましたが、これについてはおそらく無条件で用いても問題ないものと思います。心配であれば軽くでいいので証明の概略を添えておきましょう。
いや〜、しんどかった…（打ち込むのが）
以上ここまで見てきた通り、この問題の後半を解く自体に相当の労力を割いてしまう可能性がある上に並大抵どころかかなりの処理能力があってさえも厳しい問題になってしまいます。ちなみにですが、このやり方よりは楽なやり方がありますので、それを紹介します。全体的なやり方は同じなのですが、\(\displaystyle \sum^{m}_{l=1} \frac{2l^2-5l+4}{4^l}\)の計算の仕方が劇的に違います。
これを計算するにあたって、参考になるであろう題材をまずは見てみましょう。部分分数分解をして打ち消しまくるやつです。
次の和を求めよ。
$$\frac{1}{1 \cdot 3}+\frac{1}{3 \cdot 5}+\frac{1}{5 \cdot 7}+ \cdots +\frac{1}{(2n-1)(2n+1)}$$
これにはもう完全にテンプレートのやり方がありますよね。最近とある動画で知りましたが中学入試にも題材として登場したことがあるそうでびっくりしましたが…。それぞれの項の形を（分数-分数）の形にしてやることで互いに打ち消し合えるパーツを作っていく方法です。ちなみにこれをこのやり方で解くと、
$$\frac{1}{1 \cdot 3}+\frac{1}{3 \cdot 5}+\frac{1}{5 \cdot 7}+ \cdots +\frac{1}{(2n-1)(2n+1)} \ \ \ \ \ \ \ \ \ \ \ \ \ \\
\begin{eqnarray}&=&\frac{1}{2}\biggl\{\biggl(\frac{1}{1}-\frac{1}{3}\biggr)+\biggl(\frac{1}{3}-\frac{1}{5}\biggr)+\biggl(\frac{1}{5}-\frac{1}{7}\biggr)+ \cdots + \biggl(\frac{1}{2n-1}-\frac{1}{2n+1}\biggr)\biggr\} \\
&=& \frac{1}{2}\biggl(1-\frac{1}{2n+1}\biggr)\end{eqnarray}$$
となりますね。おそらく基礎問題を通しでこなしてきた人であれば誰でも知っているでしょう。これと似た手法を利用します。
今回の問題でもパーツを打ち消し合える関係に持っていきたいので、恒等式を利用して
$$\frac{2l^2-5l+4}{4^l} = \frac{a(l+1)^2+b(l+1)+c}{4^{l+1}} – \frac{al^2+bl+c}{4^l}$$
が\(l\)の値にかかわらず成り立つように定数\(a,b,c\)の値を定めます。そうすると各係数ごとの連立方程式
$$\left\{ \begin{array}{1}a-4a=8 \\ 2a+b-4b=-20 \\ a+b+c-4c=16\end{array}\right.$$
を解いて\(\displaystyle a= -\frac{8}{3}\)、\(\displaystyle b= \frac{44}{9}\)、\(\displaystyle c= -\frac{124}{27}\)が求められます。これを用いると先ほどの部分分数分解で同じ部分が丸ごと消えていたように、
$$\begin{eqnarray}\sum^{m}_{l=1} \frac{2l^2-5l+4}{4^l} &=& \sum^{m}_{l=1} \biggl\{\frac{a(l+1)^2+b(l+1)+c}{4^{l+1}} – \frac{al^2+bl+c}{4^l}\biggr\}\\
&=& \frac{a(m+1)^2+b(m+1)+c}{4^{m+1}} – \frac{a+b+c}{4} \\
& \rightarrow &-\frac{1}{4}(a+b+c) = -\frac{1}{4}\biggl(-\frac{8}{3}+\frac{44}{9}-\frac{124}{27}\biggr) = \frac{16}{27}\ \ \ (n \rightarrow \infty)\end{eqnarray}$$
という要領で求めることができます。先ほどのアレよりは楽ですが、こちらでやったとしても何とも面倒です。こうしたやり方は一見煩雑に見える処理においてもかなり計算の量が減るような特性を持っていますのでぜひ強力な武器として頭の中にインストールしておくことをお勧めします。
まとめ
ここまで処理量がえげつないような問題を見てきましたが、問題はこうした問題に当たった時にどう対処するかです。こうした問題は時間をかけこそすれば解くことはできるけど実際の試験という状況下においてここまで出なくても計算ミスをせず正しい答えにたどり着くというのは相当至難の技です。しかし、点数や戦略によってはあえて難問と思しき問題に手を出さず、より確実にとっていけるであろう問題に注力する場合がいい時もあります。
当然すんなりとこうした問題を通過できるほどの処理力を備えていることが望ましいですが、それをいかに戦略でカバーするかという判断もこの問題からは問われているように自分は改めて感じました。現に自分は過去問を１年ごとに解いていてこの問題に当たった時に、この問題に相当時間を割いて焦った挙句他で痛い目を見た記憶があります。受験生はそろそろ過去問の演習に入る頃でしょうし、過去問演習をする際には全体としての時間関係等にも意識しながら一問一問に取り組んでみてください。
コメント